7766. Коробки с сувенирами

Идет последнее действие церемонии открытия IOI 2015. Во время последнего действия каждая команда должна получить коробку с сувениром от страны организатора олимпиады. Но все волонтеры настолько увлечены церемонией, что совсем забыли про сувениры. Единственным человеком, который не забыл про сувениры, оказался Аман. Он большой энтузиаст и хочет, чтобы все команды IOI получили сувениры, при этом он хочет раздать все сувениры за наименьшее время.

Зал, где проводится церемония открытия, является круглым и разделен на l одинаковых секторов. Все секторы пронумерованы последовательно от 0 до l – 1. Таким образом, для всех i (0 ≤ i ≤ l – 2) сектор с номером i является соседним c сектором i + 1, а сектор с номером l – 1 соседний с сектором 0. В зале находятся n команд. Каждая команда сидит в одном из секторов. Каждый сектор может вместить любое количество команд. Некоторые секторы могут быть пустыми.

Имеется n одинаковых сувениров. Изначально Аман и все сувениры находятся в секторе с номером 0. Аман должен выдать один сувенир каждой команде и после того, как он отдаст последний сувенир, вернуться в сектор 0. Заметим, что в секторе 0 также могут находиться команды.

В любой момент времени Аман может нести не более k сувениров. Он должен взять сувениры в секторе 0, и это происходит мгновенно. Каждый сувенир нужно нести, пока он не будет передан одной из команд. Когда Аман несет один или более сувениров и достигает сектора, в котором находятся команды, не получившие сувениры, он может выдать по одному сувениру одной или нескольким командам, не получившим сувенир. Это также происходит мгновенно. Единственное, что требует времени – это передвижение Амана между секторами. Аман может двигаться по кругу в обоих направлениях. Переход Амана в соседний сектор (как по часовой так и против часовой стрелки) занимает ровно одну секунду, независимо от количества сувениров, которые он несет.

Ваша задача найти наименьшее количество секунд, необходимое Аману для доставки всех сувениров и возвращения в начальную позицию.

Пример. В этом примере три команды (n = 3) и 8 секторов (l = 8), а Аман может держать в руках два сувенира (k = 2). Команды находятся в секторах с номерами 1, 2 и 5.

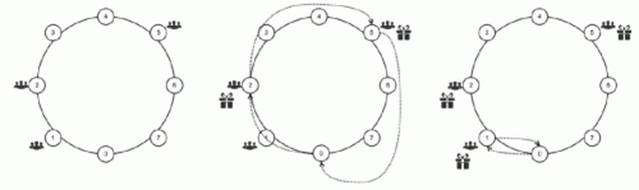
Одно из оптимальных решений показано на рисунке. За первый проход Аман берет два сувенира, передает один сувенир команде в секторе 2, второй – команде в секторе 5, а затем возвращается в сектор 0. Этот проход занимает у него 8 секунд. За второй проход Аман доставляет оставшийся сувенир команде в секторе 1 и возвращается в сектор 0. На это он тратит еще 2 секунды. Суммарное время доставки 10 секунд.

Вход. Первая строка содержит три числа: количество команд n, максимальное количество сувениров, которое может держать в руках Аман k и количество секторов в зале проведения церемонии открытия l (1 ≤ n ≤ 10⁷, 1 ≤ k ≤ n, 1 ≤ l ≤ 10⁹). Вторая строка содержит массив positions длины n. Элементы массива positions₀, ..., positions_n-1 задают номера секторов, в которых находится каждая команда. Элементы массива positions упорядочены в неубывающем порядке.

Выход. Вывести наименьшее количество секунд, которое необходимо Аману для выполнения задачи.

Пример входа	Пример выхода
3 2 8 1 2 5	10

РЕШЕНИЕ

жадные алгоритмы

Анализ алгоритма

Проходом будем называть движение Амана между последовательными посещениями сектора 0 (который будем называть базой, так как изначально здесь находятся сувениры). Во время одного прохода при оптимальном разносе подарков никакой сегмент не будет пройден в одном направлении более одного раза. Проходы можно разделить на три вида:

· CW проходы: двигаемся от 0 по часовой стрелке до некоторого сектора, после чего возвращаемся на базу против часовой стрелки.

· CCW проходы: двигаемся от 0 против часовой стрелки до некоторого сектора, после чего возвращаемся на базу по часовой стрелке.

· Круговые проходы: проход по полному кругу в любом направлении.

Лемма. В оптимальном решении длина CW и CCW проходов не превышает половины круга (l / 2).

Действительно, если в некотором CW проходе следует двигаться по часовой стрелке больше чем полкруга, то дешевле возвращаться не двигаясь назад, а двигаясь в том же направлении.

В оптимальном решении при каждом проходе разнос подарков производится в соседние (рядом расположенные) сектора.

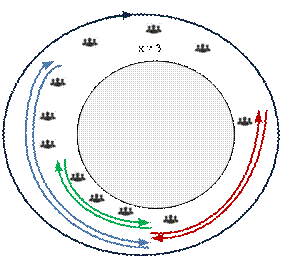
В оптимальном решении существует не более одного кругового прохода. Причем если такой имеется, то в нем следует разнести как можно больше сувениров, то есть k.

Пусть cw[i] – наименьшее время, за которое можно разнести подарки всем командам на пути от нулевой до i-ой двигясь по часовой стрелке. Соответственно cсw[i] – наименьшее время разноса подарков от нулевой до i-ой при движении против часовой стрелки.

В случае отсутствия кругового движения при оптимальном разносе подарков существует такой индекс i, что для минимизации времени следует разнести подарки двигаясь от нулевого до i-ого по часовой стрелке, а затем от нулевого до (i + 1)-го против часовой стрелки.

Если круговое движение возможно, то оно будет одно.

Рассмотрим алгоритм построения массива cw. Если i ≤ k, то разнести все подарки до i-ой команды можно зпа один раз, пройдя путь 2 * pos[i] (идем по часовой стрелке от базы до i-ой команды и обратно). Если i > k, то за последний проход выгодно разнести как можно больше подарков, то есть k. На разнос последних k подарков следует потратить 2 * pos[i] времени, а на разнос предыдущих i – k подарков следует потратить cw[i – k] времени. То есть

cw[i] = 2 * pos[i] при i ≤ k,

cw[i] = cw[i – k] + 2 * pos[i] при i > k

Пример

Реализация алгоритма

#include <cstdio>

#include <algorithm>

#define MAX 10000010

using namespace std;

int i, n, k, l;

long long pos[MAX];

long long cwdis[MAX];

// minimum distance only going clockwise giving i pep

long long ccwdis[MAX];

int main(void)

{

scanf("%d %d %d",&n,&k,&l);

for(i = 1; i <= n; i++)

scanf("%lld",&pos[i]);

cwdis[0] = 0;

for(i = 1; i <= n; i++)

cwdis[i] = ((i > k) ? cwdis[i - k] : 0) + pos[i] * 2;

ccwdis[n+1] = 0;

for(i = n; i > 0; i--)

ccwdis[i] = ((n - i + 1 > k) ? ccwdis[i + k] : 0) +

(l - pos[i]) * 2;

long long ans = min(cwdis[n],ccwdis[1]);

for(i = 1; i < n; i++)

ans = min(ans, cwdis[i] + ccwdis[i + 1]);

for(i = 1; i + k - 1 <= n; i++) // one circle for [i, i + k - 1]

ans = min(ans, cwdis[i - 1] + l + ccwdis[i + k]);

printf("%lld\n",ans);

return 0;

}

Реализация алгоритма – через указатели

Объявим указатели на рабочие динамические массивы.

long long *pep;

long long *cwdis;

long long *ccwdis;

void solve(void)

{

for(int i = 0; i < n; i++)

{

long long lstdis;

if( i + 1 > k ) lstdis = cwdis[i + 1 - k];

else lstdis = 0;

cwdis[i + 1] = lstdis + pep[i] * 2;

}

for(int i = n - 1; i >= 0; i--)

{

long long lstdis;

if (n - i > k) lstdis = ccwdis[n - i - k];

else lstdis = 0;

ccwdis[n - i] = lstdis + (l - pep[i]) * 2;

}

long long ans = 100000000000000000LL;

for(int i = 0; i <= n; i++)

ans = min(ans, cwdis[i] + ccwdis[n - i]);

for(int i = 1; i + k - 1 <= n; i++)

// one circle for [ i, i + k - 1 ] cw

ans = min(ans, cwdis[i - 1] + l + ccwdis[n - ( i + k - 1 )]);

printf("%lld\n",ans);

}

Основная часть программы. Читаем входные данные. Выделяем память под массивы. Обнуляем ее.

scanf("%d %d %d",&n,&k,&l);

pep = new long long[n + 1]; memset(pep,0,(n + 1)*sizeof(long long));

cwdis = new long long[n + 1];

memset(cwdis,0,(n + 1)*sizeof(long long));

ccwdis = new long long[n + 1];

memset(ccwdis,0,(n + 1)*sizeof(long long));

for(int i = 0; i < n; i++)

scanf("%lld",&pep[i]);

Вычисляем и выводим ответ.

solve();

Освобождаем память.

delete[] pep;

delete[] cwdis;

delete[] ccwdis;